Построение теней на C#. Часть 3
Прежде чем мы начнем, хочу поблагодарить всех за замечательные коментарии к предыдущим двум постам. Я обновлю алгоритм, чтобы постараться сделать еще лучшее круг видимости, основываясь на комментариях. Как я упоминал, есть множество тонких моментов в этих алгоритмах, и я пока только изучаю их.
Для этого в сегодняшнем эпизоде я собираюсь посвятить всю длинную статью, анализируя единственную операцию деления. Вы предупреждены.
Перед тем как мы начнем, немного жаргона. Ячейку, которая невидима, хотя по нашим физическим представлениям, должна быть видима, и ячейку, которая видима, хотя должна быть невидима, будем называть «артефактом». «Артефакт» – продукт нашего алгоритма (или деталей реализации), не достаточно аккуратно моделирующего физику реального мира. Вся сегодняшняя статья будет посвящена артефактам.
Рабочей лошадкой, реализующей алгоритм поля видимости, является метод, о котором рассказывалось в прошлый раз:
private static void ComputeFoVForColumnPortion(
int x,
DirectionVector
topVector,
DirectionVector bottomVector,
Func<int, int, bool>
isOpaque,
Action<int, int> setFieldOfView,
int
radius,
Queue<ColumnPortion> queue)
{
Он имеет два основных назначения. Во-первых, предполагается, что все точки фрагмента столбца х, ограниченного верхним и нижним векторами, находятся в поле зрения, и помечаются соответственно; некоторые из них могут быть вне радиуса видимости, но остальные по предположению видимы из начала. Во-вторых, алгоритм определяет, какая часть столбца х+1 находится в поле зрения и добавляет ее в очередь для последующей обработки.
Мы описали алгоритм, как работающий сверху вниз во фрагменте рассматриваемого столбца. Поэтому самым первым вопросом, на который мы должны ответить, станет «какая точно ячейка располагается наверху фрагмента столбца с данным номером и верхним вектором направления?»
Если так случится, что центр ячейки в столбце х окажется точно на направлении верхнего вектора, то совершенно ясно, что это и есть верхняя ячейка. Предположим для простоты, что так и есть. Тогда верхняя ячейка вычисляется x * topVector.Y / topVector.X. Деление выполняется точно. Доказательство требует некоторого владения алгеброй, и мы оставим его в качестве упражнения.
Возможно, мы должны заявить, что даже если деление является неточным, мы вычисляем верхнюю ячейку следующим образом:
int topY = x * topVector.Y / topVector.X;
(Заметим, что здесь полагается, что числа, которые мы умножаем и делим, малы по сравнению с допустимым диапазоном целых чисел, и поэтому нет никакого переполнения.)
Что случиться если деление будет неточным? Мы знаем, что в C# неточное целое деление всегда округляется по направлению к нулю; оно округляется вниз, если необходимо.
Округление вниз – неудачная идея, поскольку плохо моделирует физический мир и приводит к крайне неприглядной картине игры. Рассмотрим следующий очень распространенный сценарий:
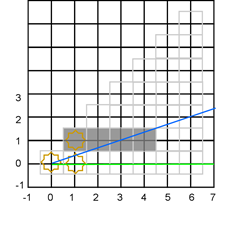
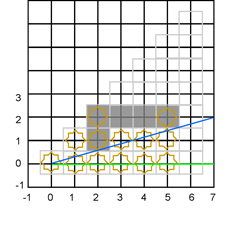
Первый сценарий
После обработки первого столбца мы опускаем наклон верхнего вектора направления до одной трети. Находится ли точка (2,1) в поле зрения? Кажется ясно, что да, поскольку вся нижняя граница ячейки находится внутри поля зрения. Но если мы посчитаем 2 * 1 / 3, то получим ноль, так что – нет, верхняя ячейка, которую можно видеть в этом столбце имеет координаты (2,0). Мы пометим ее как видимую и продолжим работу с третьим столбцом, не меняя наклона вектора. Теперь верхний вектор направления пересекает центр ячейки (3,1), так что она и ячейка (3, 0) видимы. Мы понижаем наклон верхнего вектора до одной седьмой, и теперь ячейка (4,1) не видима снова из-за округления вниз. После обработки всех столбцов, показанных здесь, состояние будет следующим:
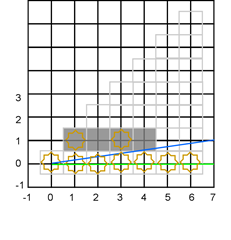
Это не соответствует ни желательной физике, ни желательному сценарию игры; прямая стена не должен иметь таинственных артефактов в виде разрывов. Заметим также, что результирующий верхний вектор также идет слегка круче; мы никогда не рассматривали непрозрачную ячейку в четвертом столбце с точки зрения возможного затенения ячеек за ней; оставшийся мир определяется лишь тенью от ячейки (3,1), а не (4,1). Округление вниз абсолютно неприемлемо.
Прекрасно. Что делать, если округление вниз не работает? Может, мы должны округлять вверх!
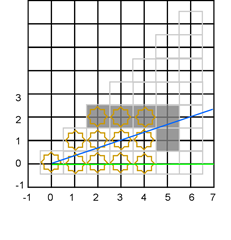
Это решает проблему длинных коридоров; теперь ячейка (2,1) определяется как видимая при округлении вверх, так что наклон верхнего вектора уменьшится до одной четвертой. После этого ячейка (3,1) определяется как видимая, и наклон уменьшается до одной седьмой. После этого ячейка (4,1) определяется как видимая, и наклон уменьшается до одной девятой. Это выглядит намного лучше.
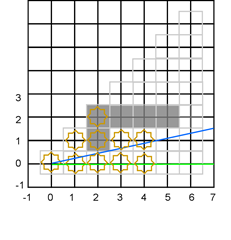
Более того, теперь мы получаем прекрасную возможность видеть углы комнаты. Рассмотрим следующую ситуацию:
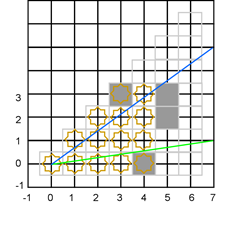
Второй сценарий
Ячейка (5,2) будет видимой, что прекрасно интерпретируется, особенно если используются символы псевдографики для рисования внутренних углов, как это и бывает в большинстве игр, подобных «rogue». Это желательный артефакт.
Но теперь у нас есть противоположная проблема; если мы округляем вверх, то потенциально можем сделать видимыми ячейки, которые должны быть в тени непрозрачных ячеек. Давайте рассмотрим пример такой ситуации:
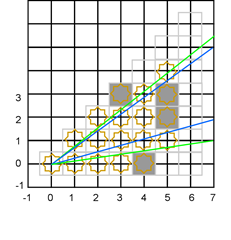
Третий сценарий
Ячейки (3,2) и (4,2) однозначно находятся в тени ячейки (2,1). Но поглядите внимательно на пятый столбец. Даже несмотря на то, что верхний вектор никак не проходит через (5,2), он проходит слегка выше точки (5,1) и поэтому при делении результат округлится так, что (5,2) окажется видимой! С этим алгоритмом округления можно слегка «заглядывать за угол». Видимая точка (5,2) – это артефакт.
Даже хуже, представьте, что случиться, когда алгоритм обнаружит, что имеется переход от непрозрачной ячейки к прозрачной между (5,2) и (5,1). Верхний вектор сдвинется вверх!
Теперь верхний вектор круче, чем должен быть. (Также отметим, что если бы он был таким при обработке четвертого столбца, то точка (4,2) должна быть видимой).
Понятно, что ситуацию можно продолжить; ошибки округления в последнем столбце можно продолжить, делая верхний вектор круче и круче. (Упражнение для читателей: существует ли максимальный наклон, которого может достичь верхний вектор за счет повторяющихся ошибок округления?)
Мы можем легко ввести в алгоритм проверку того, чтобы верхний вектор направления никогда не изменялся от пологого наклона к более крутому. Если мы примем решение всегда округлять вверх, то мы можем так сделать. Но это плохой выбор. Рассмотрим следующий сценарий, который я уже упоминал в прошлый раз:
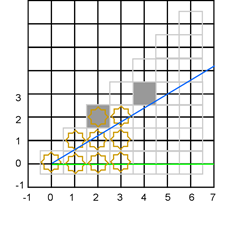
Четвертый сценарий
В прошлый раз я сделал упрощающее предположение, что ячейка (5,4) не входит в радиус видимости, и потому не видна. Но давайте предположим, что радиус видимости больше, и детально проанализируем ситуацию. Я буду округлять вверх, чтобы определить самую верхнюю видимую ячейку во фрагменте столбца, ограниченного этими векторами, так что ячейка (5,4) оказывается видимой. Затем мы посчитаем переходы от видимой (5,4) к непрозрачной (5,3) и непрозрачной (5,2) к видимой (5,1) (предполагая, что (5,1) – нижняя ячейка фрагмента; мы обсудим это предположение в следующий раз). Таким образом, мы должны поделить этот фрагмент на два подфрагмента для шестого столбца. Чтобы вычислить верхний фрагмент мы сохраним верхний вектор и передвинем нижний вектор вверх; чтобы вычислить нижний фрагмент мы сохраняем нижний вектор и опускаем верхний. В результате получаем чертовский беспорядок:
Верхний направляющий вектор верхнего фрагмента столбца оказывается теперь под нижним вектором. Супер!
Эта ошибка опять позволяет игроку «заглянуть за угол» сверхъестественным способом, но в реальности, всё не так плохо. Самое плохое, что при этом случится, так это пока перепутанные векторы определяют одну ячейку, как верхнюю и нижнюю ячейку видимого фрагмента данного столбца, то эта единственная ячейка будет видимой. Как только фрагмент станет достаточно большим, чтобы верхняя и нижняя ячейки разошлись, цикл от верхней до нижней ячейки немедленно завершится.
Опять же, мы в состоянии предотвратить эту ситуацию, выполняя проверку того, что нижний вектор никогда не оказался над верхним. Однако, возможно мы решим, что такая ситуация довольно редка, а артефакт достаточно доброкачественный, чтобы допустить его.
Округление вверх выглядит лучше округления вниз, но все равно не идеально. Хмм. А что если попробовать округлять к ближайшей точке решетки?
Первый сценарий не изменяется. Мы по-прежнему правильно вычисляем видимость всей длинной прямой стены.
Второй сценарий не изменяется. Мы по-прежнему получаем желательный «угловой артефакт».
Сценарий три улучшается. Ячейка (5,2) не трактуется, как видимая, что хорошо, поскольку она полностью в тени. Верхний вектор не становится более крутым.
Сценарий четыре не меняется. Мы по-прежнему попадаем в ситуацию, где верхний и нижний векторы меняются местами.
Итак, три сценария не изменились, а один значительно улучшился, так что это явная победа, правильно?
Не совсем. Рассмотрим следующий сценарий:
Сценарий пять
Если округлять к ближайшему, то (4,3) становится не видимой, несмотря на то, что полные 30 % нижней стороны ячейки видны из начала. Более того, не считая эту ячейку видимой, мы не можем понизить наклон верхнего вектора с 3/5 to 5/9, и, возможно, позволяем быть видимыми большему числу ячеек в последующих столбцах, которые должны затеняться ячейкой (4,3). Округление вверх трактует (4,3), как верхнюю ячейку фрагмента, в то время как округление к ближайшему не дает однозначного выигрыша над округлением вверх.
С этой точки зрения разумно сделать шаг назад и спросить себя, является ли продолжение разбора, как округлять результаты деления, правильным. Когда предлагается три разных правдоподобных способа вычислений, и все они ведут себя по-разному плохо, может быть где-то сделано неверное предположение.
Во-первых, неверное предположение состоит в том, что y = SomeKindOfRoundingOf(x, top.Y, top.X) – это правильное выражение. Это не так. Это вычисление, не важно, как выполняется округление, по существу вычисляет, где вектор пересекает центр столбца. Почему именно центр столбца имеет значение? Ведь тени отбрасывают края ячейки!
Что мы хотим посчитать, так это «какова самая верхняя ячейка в данном столбце, которая где-нибудь пересекается верхним вектором направления?» Наклон верхнего вектора направления всегда положительный; линия всегда наклонена вверх, так что верхняя ячейка может быть определена вычислением, где вектор покидает столбец. Всё, что требуется сделать, так это определить пересечение вектора с линией х+0,5, а не х.
Как мы это собираемся сделать? Во-первых, заметим, что (x + 0.5 ) * top.Y / top.X, это то же самое, что и (2 * x + 1) * top.Y / (2 * top.X). Теперь все числа целые. Давайте работать с частным и остатком в целых числах:
int quotient = ((2 * x + 1) * top.Y) / (2 * top.X);
int remainder = ((2 * x + 1) * top.Y) % (2 * top.X);
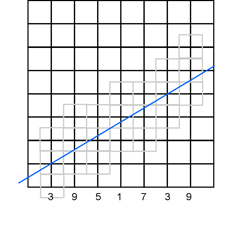
Рассмотрим набор разных возможностей. Предположим, что вектор направления (5,3), так что мы идем на пять единиц вправо и на три вверх. Интересными точками являются точки, где вектор выходит из столбца с правой стороны. Частное – число целых полос между черными горизонтальными линиями ниже интересующей точки. В этом примере остаток – это число десятых долей, на которое интересующая точка превышает линию частного. (Десятые, потому что знаменатель равен 5 x 2.) Числа внизу каждого столбца – это остатки:
(Заметим, что делимое всегда будет нечетным, а делитель – всегда четным числом, и поэтому остаток всегда будет нечетным числом. Доказательство этих утверждений оставим в виде упражнения. Подсказка: какие возможные значения y может принимать верхний вектор направления, если он ограничен только целыми числами?)
Итак, как же мы должны округлять? Рассмотрим столбцы, обозначенные 1 и 3. В этих случаях округленное вниз частное правильно определяет ячейку, которую пересекает вектор направления. В столбцах, обозначенных 7 и 9, имеется проблема; частное на единицу ниже правильного результата; мы округляем вниз неправильно. Как обстоит дело со столбцом, обозначенным 5? Если остаток точно равен значению «пробега» верхнего вектора направления, то вектор проходит точно через границу двух смежных ячеек; которая из них должна быть видима? Так как это верхний окаймляющий вектор, мы должны округлять вниз; у верхней ячейки нет видимой области.
Итак, в остатке: используйте округление вниз частного для верхней ячейки, если остаток равен top . X или меньше, в противном случае округляйте вверх, добавляя к частному единицу.
Решает ли это наши проблемы?
Первый сценарий: Хорошо. Мы правильно помещаем всю стену коридора в поле зрения.
Второй сценарий: Хорошо. Мы «правильно» помещаем ячейку невидимый угол в поле зрения.
Третий сценарий: Хорошо. Ячейка (5,2) не определяется как видимая, и поэтому наклон верхнего вектора не увеличивается.
Сценарий четыре: Плохо. Мы неправильно определяем ячейку (5,4) как видимую через ячейку (5,3), и потому получаем не только артефакт, но и перевернутый набор верхних и нижних векторов для следующего столбца.
Сценарий пять: Хорошо. Мы делаем ячейку (4,3) видимой и соответственно уменьшаем наклон верхнего вектора.
Этот алгоритм не идеален, мы по-прежнему получаем артефакты. Как можно решить проблему для сценария четыре?
На ум приходит пара способов. Один состоит в проверке входит ли вектор направления в колонку в ячейке (5,3) и выходит в (5,4) Если это так, то (5,4) – единственная верхняя ячейка, если (5,3) прозрачна.
Другой способ – позволить ячейке (5,4) быть видимой не взирая ни на что – это может иметь прекрасные свойства для показа углов, даже если технически ячейка является артефактом – но для определения, является ли новый нижний вектор круче, чем старый верхний вектор и не допускает рекурсию.
В своей реализации я решил, что решение проблемы четвертого сценария не представляет ценности; я допускаю наличие артефактов и инвертированных диапазонов. Результат выглядит вполне пристойно.
Как я и предупреждал, получилась крайне длинная статья с девятью сложными диаграммами, для постижения как разделить два числа, чтобы определить верхнюю ячейку. Я предупреждал, что она будет чрезмерно детальной!
В следующий раз мы проведем аналогичный анализ для определения нижней ячейки фрагмента столбца. К счастью это пройдет немного быстрее, поскольку у нас есть основная идея, как округление производит артефакты.